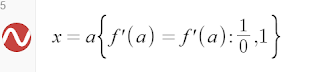Drawing vertical tangents when the gradient is undefined.

A common thing that I want to do in Desmos is draw a tangent line to a function that a user can drag around or animate. A simple way I have been using is below:

Problem

There is a slightly annoying problem with this method: If the derivative is undefined at a point then the graph won't display a vertical tangent; it just won't draw a line at all here.

Solution

I recently found a way to test for undefinedness in Desmos. The expression {k = k: 0, 1} will return 1 if k is undefined (or 0 if it's defined). So we can use this technique to graph a separate vertical line at x = a when the value of f'(a) is undefined.

Note that if the gradient is defined, I actually don't want this line to appear at all, which is why I threw in an undefined value (if I just put 0 here then it would graph x = 0 for these values of a).

I am much happier with this version of the graph.

[Update] Minor Technical Problem: Undefined function values

After posting this, I realised that the additional rule will also graph a vertical line when the function itself is undefined at a point. I'm not sure what the best behaviour is for this case, but perhaps it would be nice to have a draggable point along the x-axis with no vertical line.

To implement this, change line 2 from (a, f(a)) to a more complicated conditional

And the vertical tangent line can be set to only appear when the function is defined but the derivative is undefined.

Transformations using Draggable Points in Desmos

Activities in Desmos allow students to interact with graphs before answering a question, and this facility allows for a more natural way of asking questions that are quite hard to ask just using pen-and-paper tests.

Imagine a point A is at (2, 1) and another point A' is at (–2, 1). What is the transformation?

With draggable points, a student could move a point A around the screen and see the image point A'. After moving the point around, the student could see that the transformation was a reflection in the y-axis.

Now imagine on the next screen, the point A is at (2, 1) and the image A' is again at  (–2, 1). But this time the student drags the point around and sees that the transformation was a horizontal translation.

Once a student has engaged with these two screens the original question can be asked, but it seems much less abstract. Imagine a point A is at (2, 1) and another point A' is at (–2, 1). What is the transformation?

This question can also be asked in Desmos, and is basically a duplicate of the previous screen where the point A is no longer draggable.

Thinking of a transformation as a function T: R² → R² could seem very abstract and hard to visualise (without an ability to see in four dimensions). By allowing the first point to be draggable we can provide a good intuition of what a transformation is.

Also, it is interesting to me that simply by changing between the dynamic versions (Screen 1 and Screen 2) and the static version (Screen 3) changes the answer.

I'm not sure how easily these concepts could be shown using a pen-and-paper quiz (one could include some points A, B, C and their images A', B', C' but this seems a bit messy and not as helpful if we want students to think of it as a function mapping any point in R² to another point in R².)

The activity shown in this post is just to show the idea but if it's helpful, you might like to copy and edit it to see how it is implemented. This is the link.

New Blog

Welcome to my blog. I have had blogs before and they never last long, so I don't hold out much hope for this one.

However, I am keen to post a few thoughts about this and that, so I thought this might be better than just tweeting them as they occur to me.

I suppose I should include various disclaimers about the views here are my own and not necessarily endorsed by my employer(s). If anyone has read this far then please assume that the disclaimer has been written correctly and appears wherever anything controversial or wrong is written.